粒子滤波详解【2/3】：采样重要性重采样滤波

贝叶斯滤波 §

问题定义 §

状态估计要解决的问题是估计机器人的状态$\mathbf{x}$，比如位置、朝向等。但是我们无法直接测量得到这个状态$\hat{x}$，我们能得到的是对这个状态的一系列带噪声的观测值。贝叶斯滤波的思路是找到关于这个状态的后验概率密度函数，根据概率分布来选取最有可能出现的值作为状态的最优估计。

状态空间模型由状态方程和观测方程组成，

$$\begin{array}{rl}{\mathbf{x}}_k& ={\mathbf{f}}_k\left({\mathbf{x}}_{k-1},{\mathbf{v}}_{k-1}\right)\\ {\mathbf{z}}_k& ={\mathbf{h}}_k\left({\mathbf{x}}_k,{\mathbf{n}}_k\right)\end{array}$$

其中$\left\{{\mathbf{x}}_k,k\in \mathbb{N}\right\}$为状态序列，$k$为离散时间。$\mathbf{f}$称为状态转移函数，$\mathbf{h}$为观测函数。${\mathbf{v}}_{\mathbf{k}}$为独立同分布的过程噪声序列，${\mathbf{n}}_{\mathbf{k}}$为独立同分布的测量噪声序列。

贝叶斯滤波是给定到当前时刻$k$的测量数据序列${\mathbf{z}}_{1:k}$，估计出当前状态${\mathbf{x}}_k$的置信度，即估计后验概率密度函数$p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k}\right)$。

令时刻$0$的初始状态为${\mathbf{x}}_0$，其后验概率密度函数即为其先验概率密度函数，$p\left({\mathbf{x}}_0\mid {\mathbf{z}}_0\right)\equiv p\left({\mathbf{x}}_0\right)$ 。一般通过经验值或者建模人为设定${\mathbf{x}}_0$的后验概率密度函数，$k$时刻过程噪声和测量噪声的概率密度函数。之后，我们可以通过预测和更新两个步骤，迭代求解$p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k}\right)$。

预测步骤 §

给定时刻$k-1$的概率密度函数$p\left({\mathbf{x}}_{k-1}\mid {\mathbf{z}}_{1:k-1}\right)$，基于状态方程可得到时刻$k$的状态${\mathbf{x}}_k$的先验概率密度函数：

$$p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k-1}\right)=\int p\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}\right)p\left({\mathbf{x}}_{k-1}\mid {\mathbf{z}}_{1:k-1}\right)d{\mathbf{x}}_{k-1}$$

上述用到了Chapman-Kolmogorov等式，且状态方程为一阶马尔可夫过程，所以$p\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_{1:k-1}\right)=p\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}\right)$ 。概率转移公式$p\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}\right)$由状态方程和${\mathbf{v}}_{\mathbf{k}-1}$概率密度函数决定，是已知的。

更新步骤 §

在时刻$k$，得到测量值${\mathbf{z}}_k$，基于贝叶斯定理，更新先验概率密度函数$p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k-1}\right)$得到后验概率密度函数：

$$p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k}\right)=\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)}$$

其中归一化常数

$$p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)=\int p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k-1}\right)d{\mathbf{x}}_k$$

似然概率密度函数$p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)$由测量方程和${\mathbf{n}}_{\mathbf{k}}$概率密度函数决定，是已知的。

非线性非高斯问题 §

贝叶斯滤波方法中，预测步骤中先验概率密度函数和更新步骤中归一化常数的求解都涉及到无穷积分，可能没有解析解。贝叶斯滤波方法只是一种思路框架，具体问题还需要在这个框架下具体分析。

为了解决积分难的问题，我们可以对模型做一些假设。

• 可以假设$\mathbf{f}$和$\mathbf{h}$是否线性，得到线性/非线性系统；
• 可以假设$\mathbf{v}$和$\mathbf{n}$是否高斯噪声，得到高斯/非高斯系统；

线性高斯问题可通过卡尔曼滤波（Kalman Filter）解决；线性非高斯问题可以通过扩展卡尔曼滤波（Extended Kalman Filter）和无迹卡尔曼滤波（Unscented Kalman Filter）解决。

最复杂的情况是非线性-非高斯情况，此时就要用到本文介绍的粒子滤波方法。其是一种无参滤波，对于待估计状态的后验概率密度函数不作任何假设，通过大量采样来逼近这个函数分布。

质点滤波 §

质点滤波（point mass filter，PMF），又称网格粒子滤波或基于网格的滤波（grid-based filtering）。假设状态空间是离散的且状态是有限的，时刻$k$可以分成$N_s$个格子$\left\{{\mathbf{x}}^i:i=1,\dots ,N_s\right\}$。为了和后文的粒子滤波的符号保持一致，符号${\mathbf{x}}_k^i$表示$k$时刻的状态${\mathbf{x}}_k$在网格${\mathbf{x}}^i$中。对于$k-1$时刻离散状态${\mathbf{x}}_{k-1}^i$，记其在$k-1$时刻测量值下的条件概率为$w_{k-1\mid k-1}^i$，即概率质量函数，

$$w_{k-1\mid k-1}^i=\mathrm{Pr}\left({\mathbf{x}}_{k-1}={\mathbf{x}}^i\mid {\mathbf{z}}_{1:k-1}\right)=p({\mathbf{x}}_k^i\mid {\mathbf{z}}_{1:k-1})$$

那么后验概率密度函数为Generalized PDF：

$$p\left({\mathbf{x}}_{k-1}\mid {\mathbf{z}}_{1:k-1}\right)=\sum _{i=1}^{N_s}{w}_{k-1\mid k-1}^i\delta \left({\mathbf{x}}_{k-1}-{\mathbf{x}}_{k-1}^i\right)$$

其中$\delta (\cdot )$为狄拉克$\delta$函数。

Generalized PDF

对于离散随机变量$\mathbf{x}$，值域为$R_X=\left\{x_1,x_2,x_3,\dots \right\}$，并且概率质量函数（probability mass function，PMF，也称离散密度函数，就是离散随机变量在特定取值上的概率值）为$P_X\left(x_k\right)$，可定义generalized PDF为：

$$f_X(x)=\sum _{x_k\in R_X}{P}_X\left(x_k\right)\delta \left(x-x_k\right)$$

对应的期望值为：

E X & =\int_{-\infty}^{\infty} x f_X(x) d x \ & =\int_{-\infty}^{\infty} x \sum_{x_k \in R_X} P_X\left(x_k\right) \delta\left(x-x_k\right) d x \ & =\sum_{x_k \in R_X} P_X\left(x_k\right) \int_{-\infty}^{\infty} x \delta\left(x-x_k\right) d x \ & =\sum_{x_k \in R_X} x_k P_X\left(x_k\right) \end{aligned}$$

那么根据预测步骤，对于$k$时刻每个离散状态${\mathbf{x}}_k^i$，记其在$k$时刻预测的先验概率为$w_{k\mid k-1}^i$：

$$\begin{array}{rl}{w}_{k\mid k-1}^i& =\mathrm{Pr}\left({\mathbf{x}}_k={\mathbf{x}}^i\mid {\mathbf{z}}_{1:k-1}\right)\\ & =\sum _{j=1}^{N_S}p({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^i)p({\mathbf{x}}_{k-1}^i\mid {\mathbf{z}}_{1:k-1})\\ & =\sum _{j=1}^{N_s}{w}_{k-1\mid k-1}^{j}p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^j\right)\end{array}$$

则预测方程为：

$$\begin{array}{rl}p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k-1}\right)& =\sum _{i=1}^{N_s}{w}_{k\mid k-1}^i\delta \left({\mathbf{x}}_k-{\mathbf{x}}_k^i\right)\end{array}$$

根据更新步骤，对于$k$时刻每个离散状态${\mathbf{x}}_k^i$，记其在$k$时刻预测的后验概率为$w_{k\mid k}^i$：

$$\begin{array}{rl}{w}_{k\mid k}^i& =\mathrm{Pr}\left({\mathbf{x}}_k={\mathbf{x}}^i\mid {\mathbf{z}}_{1:k}\right)\\ & =\frac{p({\mathbf{z}}_k^i\mid {\mathbf{x}}_k^i)p({\mathbf{x}}_k^i\mid {\mathbf{z}}_{1:k-1})}{{\sum }_{j=1}^{N_S}p({\mathbf{z}}_k^i\mid {\mathbf{x}}_k^i)p({\mathbf{x}}_k^i\mid {\mathbf{z}}_{1:k-1})}\\ & =\frac{w_{k\mid k-1}^{i}p({\mathbf{z}}_k^i\mid {\mathbf{x}}_k^i)}{{\sum }_{j=1}^{N_S}{w}_{k\mid k-1}^{i}p({\mathbf{z}}_k^i\mid {\mathbf{x}}_k^i)}\end{array}$$

则更新方程为：

$$p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k}\right)=\sum _{i=1}^{N_s}{w}_{k\mid k}^i\delta \left({\mathbf{x}}_k-{\mathbf{x}}_k^i\right)$$

上述迭代过程中要求$p({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^j)$和$p({\mathbf{z}}_k^i\mid {\mathbf{x}}_k^i)$是已知的，仅需要考虑如何设置网格大小和密度。

但PMF在处理高维空间问题捉襟见肘。一是其网格表示在高维稀疏空间是低效的。比如对于100维状态变量，假设每个维度${\mathbf{x}}_i$，采样点为$-1,1$，$Pr({\mathbf{x}}_i=1)=1,Pr({\mathbf{x}}_i=-1)=0$，那么我们真正有效的采样比例为$1/(2^{1}00)=7.9e^{-31}$，采样效率是非常低的。二是多维卷积运算复杂度为$O(N_s^2)$，随着采样点增多而急剧增大。三是网格的划分不能动态变化，网格密度是预先定义好的，对于高概率密度区域不能给予高分辨率采样。为了解决以上问题，接下来介绍粒子滤波。

粒子滤波 §

序贯重要性采样（SIS） §

粒子滤波和PMF类似，也是通过采样近似后验概率密度函数。主要改进点有以下几项：

1. 粒子滤波通过动态随机网格${\mathbf{x}}_k^i$取代了PMF中的确定性网格${\mathbf{x}}^i$，从而更加灵活得表示状态空间；
2. 粒子滤波考虑所有历史状态${\mathbf{x}}_{1:k}$，而PMF仅估计当前状态${\mathbf{x}}_k$。粒子滤波处理的后验概率密度函数为$p\left({\mathbf{x}}_{0:k}\mid {\mathbf{z}}_{1:k}\right)$，对应的随机采样记为${\left\{{\mathbf{x}}_{0:k}^i,w_k^i\right\}}_{i=1}^{N_s}$。其中$\left\{{\mathbf{x}}_{0:k}^i,i=0,\dots ,N_s\right\}$为粒子集合，$\left\{w_k^i,i=1,\dots ,N_s\right\}$为对应的粒子权重，$w_k^i=\mathrm{Pr}\left({\mathbf{x}}_{0:k}={\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k-1}\right)=p\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)$，${\mathbf{x}}_{0:k}=\left\{{\mathbf{x}}_j,j=0,\dots ,k\right\}$为到$k$时刻的状态轨迹。其中粒子权重满足${\sum }_i{w}_k^i=1$。时刻$k$的后验概率密度函数可近似为：$p\left({\mathbf{x}}_{0:k}\mid {\mathbf{z}}_{1:k}\right)\approx {\sum }_{i=1}^{N_s}{w}_k^i\delta \left({\mathbf{x}}_{0:k}-{\mathbf{x}}_{0:k}^i\right)$
3. 粒子滤波中网格是根据上一篇文章蒙特卡洛估计中的重要性采样来更新的，PMF网格不会更新。重要性采样的建议分布为$x^i\sim q(x),i=1,\dots ,N_s$，$q(x)=q\left({\mathbf{x}}_{0:k}\mid {\mathbf{z}}_{1:k}\right)$，则权重应调整为$w_k^i\propto \frac{p\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}{q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}$ 理论上，我们可以基于贝叶斯滤波方法，类似于PMF预测和更新方程走一遍，迭代估计$p\left({\mathbf{x}}_{0:k}\mid {\mathbf{z}}_{1:k}\right)$。但是需要注意的是，我们现在处理的是${\mathbf{x}}_{0:k}$的多维随机变量，远不是PMF中的“一维”随机变量。每当新的观测到来时，都要对这个多维随机变量重新计算权重，随着时间推移，这个计算量将非常大。我们希望能够通过边缘分布，将粒子集合的批量采样转换成单个粒子的序贯采样，也就是序贯重要性采样（Sequential Importance Sampling，SIS）算法。

我们尝试找出$w_k^i$的递推形式。

$$\begin{array}{rl}{w}_k^i& \propto \frac{p\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}{q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k}\right)}{p\left({\mathbf{z}}_k,{\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k,{\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_k,{\mathbf{x}}_{0:k-1}^i,{\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{0:k-1},{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_{0:k-1}^i,{\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{0:k-1}^i,{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_{0:k-1}^i\mid {\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_{0:k}^i,{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{0:k-1}^i,{\mathbf{z}}_{1:k-1}\right)p\left({\mathbf{x}}_{0:k-1}^i\mid {\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k^i\right)p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^i\right)p\left({\mathbf{x}}_{0:k-1}^i\mid {\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\end{array}$$

以上推导基于贝叶斯公式、马尔可夫状态独立性假设和马尔可夫观测独立性假设。

建议分布$q\left({\mathbf{x}}_{0:k}\mid {\mathbf{z}}_{1:k}\right)$可分解为：

$$q\left({\mathbf{x}}_{0:k}\mid {\mathbf{z}}_{1:k}\right)=q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{0:k-1},{\mathbf{z}}_{1:k}\right)q\left({\mathbf{x}}_{0:k-1}\mid {\mathbf{z}}_{1:k-1}\right)$$

考虑到系统的马尔科夫性，有

$$q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{0:k-1},{\mathbf{z}}_{1:k}\right)=q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_k\right)$$

可知，$k$时刻建议分布仅依赖于${\mathbf{x}}_{k-1}$和${\mathbf{z}}_k$。代入得到权重更新方程：

$$\begin{array}{rl}{w}_k^i& \propto \frac{p\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}{q\left({\mathbf{x}}_{0:k}^i\mid {\mathbf{z}}_{1:k}\right)}\\ & =\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k^i\right)p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^i\right)p\left({\mathbf{x}}_{0:k-1}^i\mid {\mathbf{z}}_{1:k-1}\right)}{p\left({\mathbf{z}}_k\mid {\mathbf{z}}_{1:k-1}\right)q\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^i,{\mathbf{z}}_k\right)q\left({\mathbf{x}}_{0:k-1}^i\mid {\mathbf{z}}_{1:k-1}\right)}\\ & \propto w_{k-1}^i\frac{p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k^i\right)p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^i\right)}{q\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^i,{\mathbf{z}}_k\right)}\end{array}$$

这意味着我们每当新的测量数据到来时，可序贯更新粒子及其权重${\left\{{\mathbf{x}}_{0:k}^i,w_k^i\right\}}_{i=1}^{N_s}$，不需要存储历史状态${\mathbf{x}}_{0:k-1}^i$和历史观测${\mathbf{z}}_{1:k-1}$。重新理解一下，我们期望复用历史状态${\mathbf{x}}_{1:k-1}$，仅采样得到新的状态${\mathbf{x}}_k$，对应的建议分布由$q\left({\mathbf{x}}_{0:k}\mid {\mathbf{z}}_{1:k}\right)$变为条件建议分布$q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_k\right)$。因此，粒子及粒子权重都可以序贯求解，对应的SIS算法总结如下：

粒子退化 §

SIS算法存在粒子退化的问题，即随着迭代次数增多，权重系数的方差逐渐变大，少数粒子具有大权重，大部分粒子权重趋近于零，从而导致大部分计算资源浪费在更新小权重粒子上。导致这个问题的原因如上一篇文章所述，是建议分布与真实分布之间的差异导致的。

粒子退化的严重程度通过有效样本数$N_{eff}$来度量，通过变异系数$c_v$来定义：

$$N_{eff}=\frac{N_s}{1+c_v^2\left(w_k^i\right)}=\frac{N_s}{1+\frac{\mathrm{Var}(w_k^i)}{{\left(\mathrm{E}(w_k^i)\right)}^2}}=\frac{N_s}{1+N_s^2\mathrm{Var}\left(w_k^i\right)}$$

可知，当所有粒子权重均相等$w_k^i=1/N_s$，$N_{eff}$可取得最大值$N_s$；当$w_k^i=1$概率为$1/N$且$w_k^i=0$概率为$1-1/N$，则$N_{eff}$取得最小值$1$。

实际求解$N_{eff}$不易，一般求其近似值：

$${\hat{N}}_{eff}=\frac{1}{{\sum }_i^{N_s}(w_k^i{)}^2}$$

其中权重为归一化后的权重。易知$1\le {\hat{N}}_{eff}\le N_s$，${\hat{N}}_{eff}$越小，则粒子退化程度越严重。在上一篇文章我们已经提到，缩小方差可以增大粒子数$N_s$，但这增大了计算量。实际主要采用两类方法：一是选择合适的建议分布；二是在SIS算法之后进行重采样。

建议分布 §

选择好的建议分布可有效减缓粒子退化问题。我们只要关注条件建议分布$q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_k\right)$，我们介绍其两种选择形式。

最优采样 §

我们观察一下可以知道，条件建议分布包含了过去的状态${\mathbf{x}}_{k-1}$和当前的观测数据${\mathbf{z}}_k$的信息。对应的，${\mathbf{x}}_k$的条件概率密度函数为$p({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_k)$。那么一个完美的条件建议分布应等于条件概率密度函数，即

$$\begin{array}{rl}q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_k\right)& =p({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_k)\\ & =\frac{p({\mathbf{x}}_k,{\mathbf{x}}_{k-1},{\mathbf{z}}_k)}{p({\mathbf{x}}_{k-1},{\mathbf{z}}_k)}\\ & =\frac{p({\mathbf{z}}_k\mid {\mathbf{x}}_k,{\mathbf{x}}_{k-1})p({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1})p({\mathbf{x}}_{k-1})}{p({\mathbf{z}}_k\mid {\mathbf{x}}_{k-1})p({\mathbf{x}}_{k-1})}\\ & =\frac{p({\mathbf{z}}_k\mid {\mathbf{x}}_k)p({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1})}{p({\mathbf{z}}_k\mid {\mathbf{x}}_{k-1})}\end{array}$$

则权重更新方程为：

$$w_k^i\propto w_{k-1}^{i}p({\mathbf{z}}_k\mid {\mathbf{x}}_{k-1}^i)$$

可知，无论${\mathbf{x}}_k$的采样值如何，其权重都是相等的。此时方差为$0$，$N_{eff}$可取得最大值。这就是最优采样的含义。

但是，最优采样是有问题的：

1. 我们基本无法从$p({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{z}}_k)$进行采样，因为我们可能不知道其形式。要是知道了，我们就不需要这么费劲做蒙特卡洛采样了；
2. 权重更新基本是不可计算的，$p\left({\mathbf{z}}_k\mid {\mathbf{x}}_{k-1}^i\right)=\int p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)p\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}^i\right)d{\mathbf{x}}_k$ 需要对整个状态空间做积分。

先验采样 §

实际上通常选用$\mathbf{x}$的条件先验概率密度函数作为建议分布：

$$q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}^i,{\mathbf{z}}_k\right)=p\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}^i\right)$$

则权重更新方程为：

$$w_k^i\propto w_{k-1}^{i}p\left({\mathbf{z}}_k\mid {\mathbf{x}}_k^i\right)$$

先验采样对于粒子及权重的更新非常简单，因此是目前应用最为广泛的。其强依赖于条件先验概率密度函数，因此当系统先验的状态转移函数相比于观测函数能提供更多信息时，先验采样效果更好。否则，应该从似然函数（观测函数）采样。

似然采样 §

选用似然函数作为建议分布：

$$q\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}^i,{\mathbf{z}}_k\right)=p\left({\mathbf{z}}_{\mathbf{k}}\mid {\mathbf{x}}_{\mathbf{k}}\right)$$

则权重更新方程为：

$$w_k^i\propto w_{k-1}^{i}p\left({\mathbf{x}}_k^i\mid {\mathbf{x}}_{k-1}^i\right)$$

似然采样要求似然函数$p\left({\mathbf{z}}_{\mathbf{k}}\mid {\mathbf{x}}_{\mathbf{k}}\right)$在${\mathbf{x}}_k$处是可积的。因为对于每个${\mathbf{z}}_k$，我们需要在可能的${\mathbf{x}}_k$的流形上进行采样，采样点概率等于似然。

重采样 §

除了选择合适的建议分布外，重采样也可以有效抑制粒子退化问题。一般而言，当有效样本数小于一个阈值${\hat{N}}_{eff}<N_T$，需要进行重采样。比如${\hat{N}}_T=2N/3$。重采样的基本思路是去除小权重粒子，聚焦于大权重粒子。也就是说重采样后，大权重粒子可能会被复制多份，小权重粒子可能直接就被删除了，如下图所示：

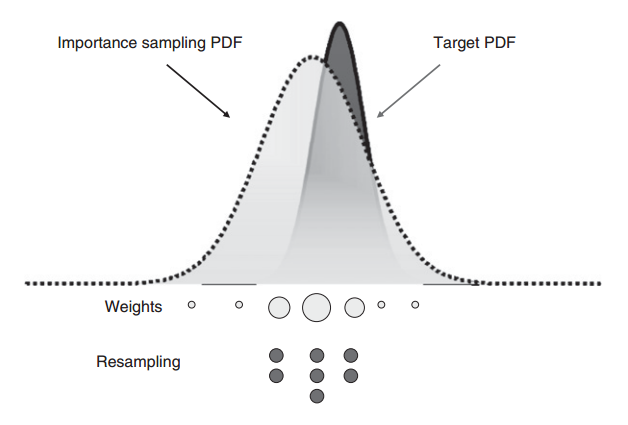
重采样操作生成新的粒子集合及粒子权重${\left\{{\mathbf{x}}_k^{\ast (j)},w_k^{\ast (j)}\right\}}_{j=1}^{N_s}$，通过对Generalized PDF $p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k}\right)$重新采样$N_s$次，使得$\mathrm{Pr}({\mathbf{x}}_k^{j\ast }={\mathbf{x}}_k^i)=w_k^i$，其中

$$p\left({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k}\right)\approx \sum _{i=1}^{N_s}{w}_k^i\delta \left({\mathbf{x}}_k-{\mathbf{x}}_k^i\right)$$

因为重新采样是对离散分布进行独立同分布采样，所以$w_k^{\ast (j)}=1/N,j=1,2,\cdots ,N_s$ .

重采样方法较多，系统重采样（Systematic Resampling）、如分层重采样（Stratified Resampling）、残差重采样（Residual Resampling）等。这里给出系统重采样的伪代码实现，其时间复杂度为$\mathcal{O}(N_s)$。

重采样带来的问题是样本贫化（Sample Impoverishment）。当粒子退化问题比较严重时，重采样后的粒子可能只包含几个重复的粒子，从而丧失了粒子多样性，无法准确近似本来的概率密度函数，最终导致发散。

基础的粒子滤波 §

将SIS与重采样组合，构成了基础的粒子滤波，这是后续多种粒子滤波变种的基础。其对应的伪代码如下：

SIR滤波 §

最后我们引出在机器人领域中常用的经典滤波算法——采样重要性重采样（Sampling Importance Resampling，SIR）滤波。其基于先验采样，并且在每个时刻都进行重采样，对应的伪代码如下：

---

参考：

1. Arulampalam M S, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on signal processing, 2002, 50(2): 174-188. PDF链接
2. Gustafsson F. Particle filter theory and practice with positioning applications[J]. IEEE Aerospace and Electronic Systems Magazine, 2010, 25(7): 53-82. PDF链接
3. 博客 - 从贝叶斯滤波到粒子滤波
4. Probability, Statistics, and Random Processes - Using the Delta Function
5. B站 - 徐亦达机器学习：Particle Filter 粒子滤波