粒子滤波详解【1/3】：蒙特卡洛估计

积分问题 §

假设我们需要求以下定积分：

$$A={\int }_a^{b}f(x)dx$$

根据微积分基本定理（也称牛顿-莱布尼兹定理），可以得到

$$A={\int }_a^{b}f(x)\mathrm{d}x={F(x)|}_a^b=F(b)-F(a)$$

其中$F(x)$是$f(x)$的任意一个原函数，即$F^{\prime }(x)=f(x)$，且要求$f$在区间$[a,b]$上连续。示意图所示：

但是存在一些情况，我们无法得到原函数，例如下图：

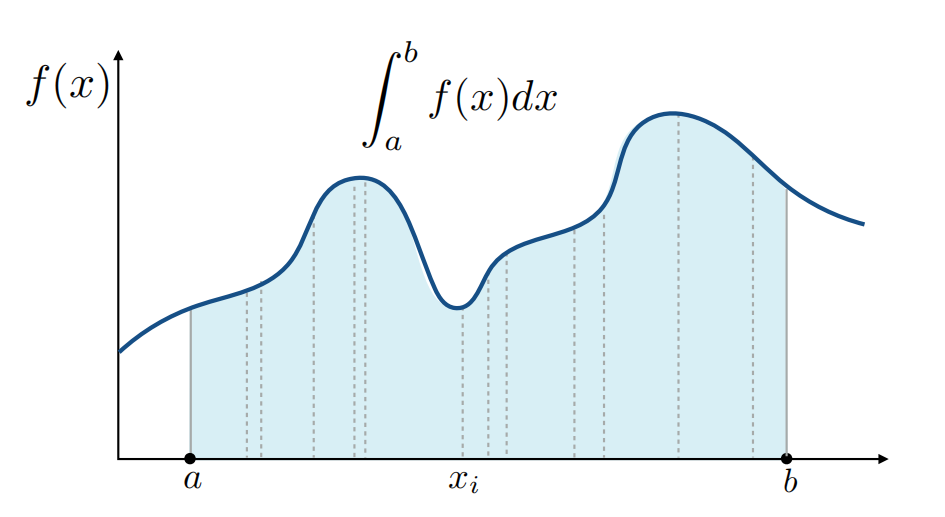
此时，我们需要借助蒙特卡洛（Monte Carlo）方法。蒙特卡洛方法指的是通过随机采样来求解数值问题。在积分上的应用体现为：利用一个随机变量对被积函数进行随机采样，通过对采样值进行处理，可以近似得到定积分值。这样，就无需关注原函数的形式，直接近似求解积分结果。

蒙特卡洛积分的思路如下图所示，我们在区间$[a,b]$中随机取一个值$x$，形成一个宽为$(b-a)$高为$f(x)$的矩形，计算$f(x)\ast (b-a)$ 为该矩形的面积。可以看到，$x1$处面积小于函数曲线的面积，$x2$处面积又大于函数曲线面积。不难想象，当我们不断地随机采样，并且将所有矩形面积相加求平均，最终的结果将会越来越接近于函数曲线的面积。

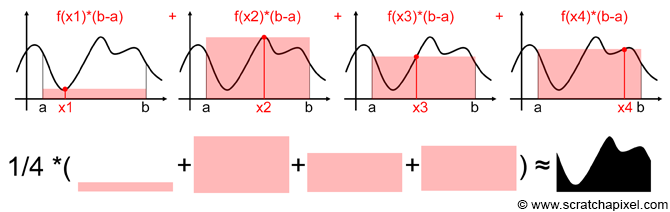
基础蒙特卡洛估计 §

假设我们要求解定积分$A={\int }_a^{b}f(x)dx$，基础蒙特卡洛估计方法为：

1. 在区间$[a,b]$上均匀采样得到样本$\left\{X_1,\dots ,X_N\right\}$，样本对应的函数值为$\left\{\mathrm{f}\left({\mathrm{X}}_1\right),\dots ,\mathrm{f}\left({\mathrm{X}}_{\mathrm{N}}\right)\right\}$。
2. 基础蒙特卡洛估计值$F_N$表达为：$F_N\approx \frac{b-a}{N}{\sum }_{i=1}^{N}f\left(X_i\right)$ 注意，$X_i$是通过均匀分布采样得到的，是随机变量且服从均匀分布$X_i\sim U[a,b]$，对应概率密度函数（Probability Distribution Function，PDF）为：

$$p(x)=\{\begin{array}{cc}\frac{1}{b-a}& a<x<b\\ 0& \text{ others }\end{array}$$

接下来证明蒙特卡洛估计值的数学期望$E\left[F_N\right]$等于被积函数的积分真值$A$，来证明其正确性。

$F_N$是$\left\{X_1,\dots ,X_N\right\}$的组合而来，也是一个随机变量，其数学期望是：

$$\begin{array}{rl}E\left[F_N\right]& =E\left[\frac{b-a}{N}\sum _{i=1}^{N}f\left(X_i\right)\right]\\ & =\frac{b-a}{N}\sum _{i=1}^{N}E\left[f\left(X_i\right)\right]\\ & =\frac{b-a}{N}\sum _{i=1}^N{\int }_a^{b}f(x)p(x)dx\\ & =\frac{b-a}{N}\sum _{i=1}^N{\int }_a^{b}f(x)\frac{1}{b-a}dx\\ & =\frac{b-a}{N}\frac{1}{b-a}\sum _{i=1}^N{\int }_a^{b}f(x)dx\\ & =\frac{1}{N}\sum _{i=1}^N{\int }_a^{b}f(x)dx\\ & ={\int }_a^{b}f(x)dx=A\end{array}$$

推导用到的数学基础公式

连续型随机变量$X$的样本空间为$D$，其PDF为$p(x)$，则数学期望计算为：

$$\mathrm{E}(\mathrm{X})={\int }_{\mathrm{D}}\mathrm{xp}(\mathrm{x})\mathrm{dx}$$

另一连续型随机变量$Y=f(X)$，则$Y$的数学期望为：

$$E(Y)={\int }_{D}f(x)p(x)dx$$

由上述推导可知，$F_N$是一个样本统计量且期望为$A$。由大数定律，$F_N$依概率收敛于$A$，即理论上随着$N$的增加，$F_N$越趋近于$A$。这也证明蒙特卡洛估计是正确的，且是一个无偏估计。

弱大数定律（辛钦定理）

样本均值${\bar{X}}_n$依概率收敛于数学期望值，即

$${\bar{X}}_n=\frac{1}{n}\sum _{k=1}^n{X}_k\stackrel{P}{\to }\mu \text{ as }n\to \infty$$

也就是对于任意$\epsilon \succ 0$，有

$$\underset{n\to \infty }{\lim }P\left\{\left|{\bar{X}}_n-\mu \right|\prec \epsilon \right\}=1$$

其中$X1,X2,\cdots$为独立同分布且数学期望$E\left(X_k\right)=\mu (k=1,2,\cdots )$皆存在且有限的随机变量构成的无穷序列。

蒙特卡洛估计的一般形式 §

进一步，我们给出蒙特卡洛估计的一般定义。上述推导是按照均匀分布采样得到的，接下来按照概率密度函数$p(x)$在区间$[a,b]$上采样得到样本集$\left\{X_1,\dots ,X_N\right\}$，蒙特卡洛估计的一般形式为：

$$F_N=\frac{1}{N}\sum _{i=1}^N\frac{f(X_i)}{p(X_i)}$$

请记住这个非常重要的表达式。

我们来直观理解一下为什么要除以$p(X_i)$。蒙特卡洛估计时，我们期望均匀采样得到$X_i$，从而构建无偏估计。但实际情况是我们不一定能对$X$做均匀分布的采样，比如给我们的就是一个任意概率密度$p(x)$的采样器。此时如果仍然按照均匀分布去采样，那么实际采样出来的$X_i$并不是均匀分布的。在PDF高的地方，样本点会过多，此时在那一部分的采样点函数值会过度累加，从而蒙特卡洛估计变成有偏。

除以$p(X_i)$其实就是添加一个权重系数。在PDF高的区域，采样点函数值的贡献会减弱。在PDF低的区域，采样点过于稀疏，这些采样点函数值的贡献需加强。

接下来验证其正确性。计算$F_N$的数学期望：

$$\begin{array}{rl}E\left[F_N\right]& =E\left[\frac{1}{N}\sum _{i=1}^N\frac{f\left(X_i\right)}{p\left(X_i\right)}\right]\\ & =\frac{1}{N}\sum _{i=1}^{N}E\left[\frac{f\left(X_i\right)}{p\left(X_i\right)}\right]\\ & =\frac{1}{N}\sum _{i=1}^N{\int }_a^b\frac{f(x)}{p(x)}p(x)dx\\ & =\frac{1}{N}\sum _{i=1}^N{\int }_a^{b}f(x)dx\\ & ={\int }_a^{b}f(x)dx=A\end{array}$$

至此，可以给出蒙特卡洛估计如下：

$${\int }_{D}f(x)dx=\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{i=1}^N\frac{f\left(X_i\right)}{p\left(X_i\right)}$$

前面通过求蒙特卡洛估计的数学期望证明了其估计出来的积分值是正确的，但是估计值与积分真值仍存在差异，用方差来描述。接下来，通过求解蒙特卡洛方法的方差，来观察其收敛性和收敛速度。 令$Y=\frac{f(X)}{p(X)}$，$F_N$的方差计算为：

$$\begin{array}{rl}{\sigma }^2\left(F_N\right)& ={\sigma }^2\left[\frac{1}{N}\sum _{i=1}^N\frac{f\left(X_i\right)}{p\left(X_i\right)}\right]=\frac{1}{N^2}\sum _i^N{\sigma }^2\left[\frac{f\left(X_i\right)}{p\left(X_i\right)}\right]\\ & =\frac{1}{N^2}\sum _i^N{\sigma }^2\left[Y_i\right]=\frac{1}{N^2}\left(N{\sigma }^2[Y]\right)\\ & =\frac{1}{N}{\sigma }^2[Y]\end{array}$$

标准差为：

$$\sigma \left[F_N\right]=\frac{1}{\sqrt{N}}\sigma [Y]$$

可知，当$N\to \infty$时，$\sigma \left[F_N\right]$趋向于0，$F_N$趋向于$A$，这说明了蒙特卡洛积分是收敛的。

蒙特卡洛积分的收敛速度和稳定性取决于$Y$。如果不同采样$X_i$导致$\frac{f(X_i)}{p(X_i)}$的值变化剧烈，则$\sigma [Y]$变大，蒙特卡洛积分的收敛速度就变慢，积分估计值不稳定。

重要性采样 §

接下来需要考虑的就是如何快速缩小蒙特卡洛估计的方差，从而降低估计误差。很直观，$\sigma \left[F_N\right]$与$N$及$\sigma [Y]$有关。一方面，我们可以增大样本数$N$，每增多四倍样本数，标准差就减少一半，但是这需要四倍计算量。我们总是希望使用一个方差较小且收敛很快的估计器，来减少计算次数。那么有没有不提高样本数也能达到减少误差的方法呢？答案是方差缩减。其中很重要的一个方法是重要性采样。

蒙特卡洛积分的核心是按照某一个概率密度函数来进行随机采样。为了减小$\sigma \left[F_N\right]$，最佳方案是不增大$N$的基础下，尽可能减小$\sigma [Y]$。可以观察到，当$p(x)=f(x)$时，$Y=1$，$\sigma [Y]=0$，$\left[F_N\right]$是一个完美的估计器。这提示我们，蒙特卡洛积分按照被积函数相似的概率密度函数来随机采样时，收敛更快且更稳定。此时，$f(x)$越大的地方，$p(x)$越大，也就是被积函数值越大的地方，采样数越多，即对重要的地方加大采样频次，把有限的采样合理分配到每个区间，这就是重要性采样。

理论上，最优的概率密度函数$p(x)$是

$$p(x)=\frac{|f(x)|}{\int f(x)dx}$$

但积分真值$\int f(x)dx$本来就是我们要去求解的，我们无法得到最完美的概率密度函数。

最后举一个例子，考虑分段函数$f(x)$，需计算其在区间$[0,10]$上的积分。

$$f(x)=\{\begin{array}{cc}4.2& 0\le x<1\\ 0.2& 1\le x\le 10\end{array}$$

容易得到其积分真值为$6$。 对于基础蒙特卡洛估计，均匀分布概率密度函数为：

$$p_1(x)=\frac{1}{10},x\in [0,10]$$

设计重要性采样蒙特卡洛估计器，随机采样概率密度函数为：

$$p_2(x)=\{\begin{array}{cc}4.2/6& 0\le x<1\\ 0.2/6& 1\le x\le 10\end{array}$$

我们简单的将$p_2(x)$由$f(x)$缩放而来，是一个完美的随机采样概率密度函数，如下图所示，显然$p_2(x)$更加符合$f(x)$曲线形态。

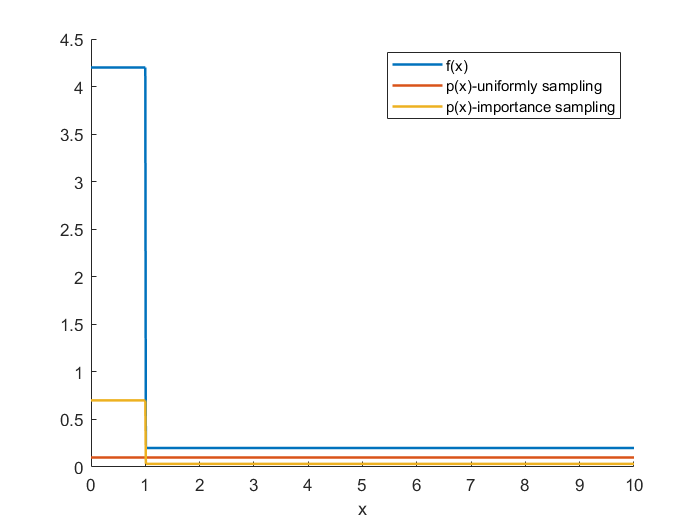
基于MATLAB代码实现以上两种概率密度函数的蒙特卡洛积分结果。代码如下：

close all; clear all; clc;
region_L = 0; region_U = 10;
x_true = region_L : 0.01 : region_U;

fx = @(x)(x<=1).*4.2 + (x>1).*0.2;
fx_int = 6;

prob1 = @(x)1/(region_U - region_L) * ones(size(x));
prob2 = @(x)fx(x)./fx_int;
rand1 = @(x)x.*(region_U - region_L);
rand2 = @(x)(x<=1)./4.2 + (x>1)./0.2;
figure; hold on;
plot(x_true, fx(x_true),'LineWidth', 1.5);
plot(x_true, prob1(x_true),'LineWidth', 1.5);
plot(x_true, prob2(x_true),'LineWidth', 1.5);
xlabel('x');
legend('f(x)','p(x)-uniformly sampling','p(x)-importance sampling')

samples = 20;
run_times = 20;
FN_1 = zeros(1, run_times);
FN_2 = zeros(1, run_times);
for run_it = 1:run_times
    for i = 1:samples
        x_sample = rand();
        sample_1 = rand1(x_sample);
        sample_2 = rand2(x_sample);
        FN_1(run_it) = FN_1(run_it) + fx(sample_1) / prob1(sample_1);
        FN_2(run_it) = FN_2(run_it) + fx(sample_2) / prob2(sample_2);
    end
    FN_1(run_it) = FN_1(run_it) / samples;
    FN_2(run_it) = FN_2(run_it) / samples;
end

disp(['均匀采样蒙特卡洛估计均值E[FN]： ', num2str(mean(FN_1)),...
    ',标准差σ[FN]:', num2str(std(FN_1))]);
disp(['重要性采样蒙特卡洛估计均值E[FN]：', num2str(mean(FN_2)),...
    ',标准差σ[FN]:', num2str(std(FN_2))]);
disp(['积分真值：', num2str(fx_int)]);

最终输出结果如下：

均匀采样蒙特卡洛估计均值E[FN]： 6.2,标准差σ[FN]:2.5874
重要性采样蒙特卡洛估计均值E[FN]：6,标准差σ[FN]:0
积分真值：6

可知，重要性采样估计值标准差小于均匀采样，符合预期。

---

参考：

1. CSDN - 蒙特卡洛积分和重要性采样(Importance Sampling)
2. 知乎 - 蒙特卡洛积分
3. Mathematics for Computer Graphics